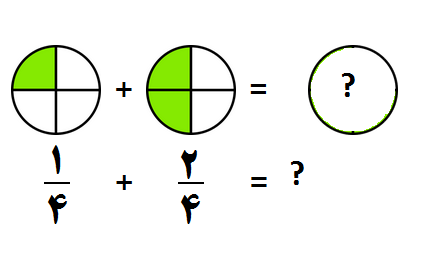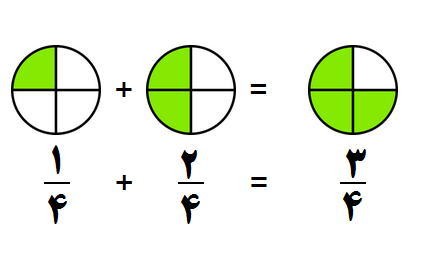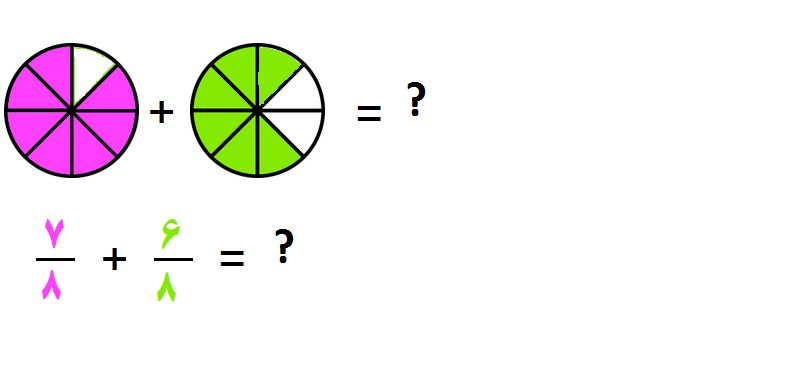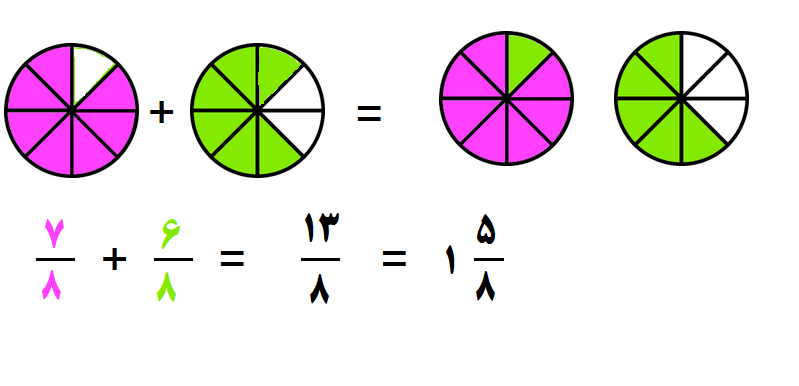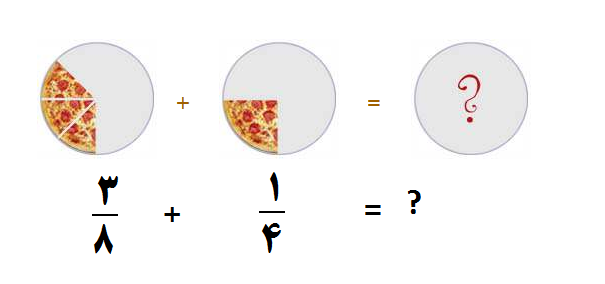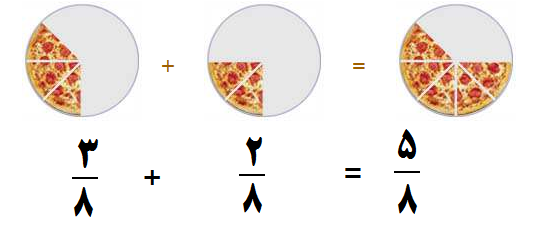آموزش جمع کسرها در ریاضی پایه ششم دبستان

جمع کسرها ششم دبستان

 

 برای جمع کسرها باید این سه مرحله را انجام دهیم:

 

• مرحله ۱: اطمینان حاصل کنید که مخرج ها یکسان هستند
  (اگر مخرج ها برابر نبودند مخرج مشترک می گیریم)

 

• مرحله ۲: یکی از مخرج ها را می نویسیم و صورت کسرها را با هم جمع می کنیم

 

• مرحله ۳: ساده کردن جواب (در صورت نیاز)

 

 

مثال ۱: کسرهای زیر را جمع کنید:

 

• مرحله ۱: چون مخرج ها یکسان هستند پس به مرحله ۲ می رویم.

•  مرحله ۲: یکی از مخرج ها را می نویسیم و صورت کسرها را با هم جمع می کنیم.

•  مرحله ۳: کسر را ساده می کنیم که در اینجا نیازی به ساده کردن نیست.

 

---

 مثال ۲: کسرهای زیر را جمع کنید.

• مرحله ۱: چون مخرج ها یکسانند (هر دو 8 هستند) پس به مرحله ۲ می رویم.

•  مرحله ۲: یکی از مخرج ها را می نویسیم و صورت کسرها را با هم جمع می کنیم.

•  مرحله ۳: کسر را ساده می کنیم که در اینجا نیازی به ساده کردن نیست ولی می توان آن را به صورت عدد مخلوط نوشت.

 

---

نکته: اگر مخرج های کسرها برابر نبودند ابتدا مخرج مشترک می گیریم.

---

مثال ۳: کسرهای زیر را جمع کنید.

چون مخرج ها برابر نیستند پس مخرج مشترک می گیریم و یکی از مخرج ها را نوشته و صورت ها را با هم جمع می زنیم.

 

جواب نهایی یعنی ۵/۸ را نمی توان ساده کرد.

آموزش جمع کسرها در ریاضی پایه ششم دبستان . آموزش جمع کسرها در ریاضی ششم . آموزش جمع کسرها ریاضی ششم دبستان

 

:: مطالب مرتبط: نمونه سوال نسبت، تناسب و درصد , نمونع سوالات اندازه گیری ریاضی ششم کد 8653 , آزمون اندازه گیری ریاضی ششم کد 8652 , کاربرگ دوران ریاضی ششم , نمونه سوالات فصل اول تا چهارم ( نوبت اول) کد 86141 , ریاضی ششم| نمونه سوالات تقارن و مختصات کد 8643 , آزمون نوبت اول ریاضی ششم ( فصل اول تا سوم) کد ۱۸۶۱ , نمونه سوال فصل اعداد اعشاری ریاضی ششم کد ۸۶۳۴ , معلم خصوصی ریاضی ششم| مرکز و شرق ۷۶۸۷۵۸۴۵ | شمال ۲۲۸۶۹۰۳۸ | غرب تهران ۴۴۴۶۹۹۲۱ , نمونه سوالات اعداد اعشاری ریاضی ششم کد ۸۶۳۳ ,

منبع : جمع کسرها

 

جمع کسر با مخرج های نامساوی

برای مخرج مشترک گرفتن بین دو کسر با مخرج های متفاوت باید کوچک ترین مضرب مشترک دو عدد (ک.م.م) را پیدا کنید.

مجموعه اعداد صحیح عبارتند از کلیه اعداد طبیعی (1، 2، 3، 4 و . . .) به انضمام صفر. به بیان ساده تر اعداد صحیح عبارتند از 0، 1، 2، 3 و 4 و . . . الی آخر. هر عددکسری، قسمتی از یک عدد صحیح است. برای مثال، 3/4  یعنی 3 قسمت از 4. دراین جا صورت کسر، 3 و مخرج کسر 4 است.

پیشتر با این مطلب که صورت کسر عددی را نشان می دهد که نشانگر تعداد یک مجموعه از کل آن مجموعه می باشد آشنا شدید.

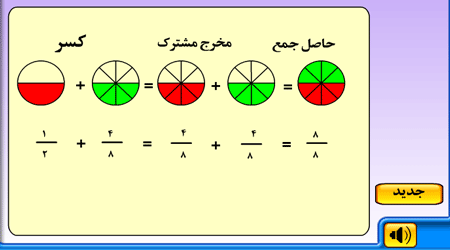
در این بازی آموزشی، دانش آموزان دوره متوسطه به خوبی با مفهوم کسر و جمع کردن عددهای کسری که مخرج آنها یکسان نمی باشند آشنا می شوند.

روی دکمه شروع کلیک کنید و سپس روی دکمه جدید کلیک کنید تا کسر نشان داده شود.

حالا دو کسر همراه با شکل رنگ شده مربوط به آن کسر را می بینید، حالا باید دو کسر را با هم جمع کنید و از آنجایی که مخرج آنها متفاوت است ابتدا باید مخرج مشترک بین آنها بگیرد (دو عدد 8 و 2 را در نظر بگیرید، مضرب های آن ها را بنویسید و از میان آن ها کوچک ترین عددی را که مضرب مشترک هر دو عدد باشد را انتخاب کنید.)

حال مضرب مشترک بین این دو کسر عدد 8 می باشد، آن را در جای خالی نوشته سپس دکمه اسپیس را از صفحه کلید فشار دهید و حالا نوبت صورت کسر است که عدد درست را بنویسید در اینجا باید مخرج عدد 8 را تقسیم بر مخرج کسر اول عدد 2 کرده حاصل را در صورت کسر که عدد 1 می باشد ضرب کنید و جواب را که عدد 4 می باشد در جای خالی نوشته و سپس دکمه اسپیس را فشار دهید.

می بینید که وقتی صورت و مخرج کسر را مشخص می کنید شکل مربوط به آن نیز به نسبت کسر رنگ آمیزی می شود، حال به همین ترتیب ادامه مسئله را حل کنید، صورت کسر بعدی نیز عدد 4 می باشد آن را وارد کرده و دکمه اسپیس را بزنید تا جواب آخر را که حاصل جمع عبارت کسری است مشاهده نمایید.

برای انجام تمرینات بیشتر روی دکمه جدید کلیک کنید و به مراحل بعد بروید.

 

جمع دو کسر با مخرج یکسان:

جمع دو کسر با مخرج یکسان از آسان‌ترین اعمال بر روی کسرها می‌باشد که برای این منظور تنها کافیست که اعداد در صورت کسرها را با یکدیگر جمع کنید. مثال زیر یک نمونه از این است که در آن اعداد مخرج هر دو کسر برابر ۸ می‌باشد، لذا تنها کافیست تا اعداد در صورت دو کسر را با یکدیگر جمع نمود که در این مثال ۷+۵=۱۲ می‌شود.